Understanding Trigonometry: The Basics
Trigonometry is a branch of mathematics that focuses on the relationships between the angles and sides of triangles, particularly right triangles. The most fundamental concepts within this discipline are the trigonometric functions: sine, cosine, and tangent. Each of these functions relates an angle in a right triangle to ratios of two of its sides, providing a foundation for solving various mathematical problems.
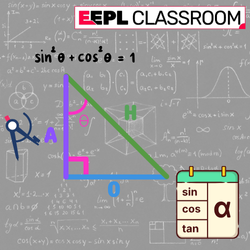
The sine function (sin) measures the ratio of the length of the opposite side to the length of the hypotenuse of a right triangle. Conversely, the cosine function (cos) calculates the ratio of the adjacent side’s length to that of the hypotenuse. Finally, the tangent function (tan) compares the length of the opposite side to that of the adjacent side. Mastery of these basic functions is essential for tackling trigonometric problems encountered in Class 9 math curriculum.
To understand the trigonometric concepts more deeply, it is crucial to study right triangles. A right triangle is characterized by one angle measuring 90 degrees. By recognizing this triangle type, students can apply the definitions of sine, cosine, and tangent effectively to various problems. Visual aids, such as diagrams illustrating the triangle with labeled sides and angles, can significantly enhance comprehension.
In addition to right triangles, the unit circle is a vital component of trigonometry. The unit circle provides a graphical representation of sine and cosine values for different angles, promoting a clear understanding of trigonometric ratios. Through this circular approach, students can visualize how these functions behave as angles vary, ultimately forming a bridge between geometry and algebra.
Through understanding these basic concepts, students can confidently approach more complex trigonometric problems presented in their Class 9 syllabus, laying the groundwork for higher mathematics.
Common Trigonometric Identities and Ratios
Trigonometric identities play a significant role in solving various problems encountered in Class 9 mathematics. These identities serve as foundational tools, enabling students to understand and simplify relationships between angles and sides in triangles. The primary trigonometric ratios—sine, cosine, and tangent—are defined in relation to a right triangle. Specifically, for an angle θ, these ratios are articulated as follows: sin(θ) = opposite/hypotenuse, cos(θ) = adjacent/hypotenuse, and tan(θ) = opposite/adjacent. Their reciprocal identities are also crucial and include cosecant (csc), secant (sec), and cotangent (cot).
Additionally, the Pythagorean identities further enrich the understanding of trigonometric relationships. The most significant Pythagorean identity states that sin²(θ) + cos²(θ) = 1, which provides a basis for various calculations and problem-solving techniques. This identity can be used to derive other Pythagorean identities, demonstrating the interconnected nature of trigonometric functions. It is essential for students to become adept at recognizing and applying these identities as they will encounter various forms of problems in their coursework.
For example, consider the problem of finding the length of a side in a right triangle given an angle and the length of one side. By using the sine or cosine ratios, students can easily derive the missing lengths. To illustrate, if a student knows the angle θ and the length of the hypotenuse, they can calculate the opposite side using the formula: opposite = hypotenuse × sin(θ). This straightforward application emphasizes how trigonometric identities streamline the problem-solving process in Class 9.
In summary, understanding common trigonometric identities and their applications will significantly enhance students’ ability to tackle trigonometric problems encountered in Class 9. Mastery of these identities not only simplifies mathematical calculations but also fosters a deeper comprehension of geometric relationships.
Problem-Solving Techniques for Class 9 Trigonometry
Mastering trigonometric problems in class 9 requires a systematic approach to problem-solving that enhances comprehension and accuracy. One effective strategy is to start by carefully reading the problem statement to identify and list all given information, as well as what needs to be found. This step ensures that students can clearly see the relationship between different elements of the problem.
Diagrams play a crucial role in visualizing the trigonometric scenario presented in problems. Drawing a right triangle, for instance, can significantly aid in understanding the relationships among the angles and side lengths. Labeling the triangle with the given values helps reinforce the concepts while providing a reference point throughout the solving process. Moreover, it allows students to apply fundamental trigonometric ratios, such as sine, cosine, and tangent, effectively.
When approaching problems, it is essential to adhere to a logical order. Start with the known information and systematically apply the relevant trigonometric formulas. Practicing the identification of which trigonometric relationship to use (whether it be for finding angles or side lengths) can enhance problem-solving skills. Common pitfalls include misinterpreting angles or neglecting to apply the correct ratio, which can lead to incorrect conclusions. To avoid these mistakes, double-check calculations and ensure that the chosen formulas are correctly aligned with the problem requirements.
To further aid students, several practice problems across varying difficulty levels should be undertaken. For example, students may encounter straightforward problems such as finding the length of the opposite side given the adjacent side and an angle, as well as more challenging ones involving angles of elevation and depression. By working through these examples, learners can solidify their understanding of trigonometric principles while developing effective problem-solving techniques necessary for class 9 success.
Real-Life Applications of Trigonometry
Trigonometry, often perceived as a purely academic subject in class 9, holds significant real-world relevance that extends beyond the classroom. Its applications are prominently seen across various fields such as architecture, engineering, astronomy, and physics. Recognizing these applications can inspire students to appreciate the subject and understand its practical importance.
In architecture, trigonometry is vital for designing buildings and structures. Architects utilize trigonometric ratios to determine heights and angles, ensuring stability and aesthetic balance. For instance, when designing a roof, an architect may need to calculate specific angles to enable effective drainage and withstand weather conditions. This application directly relates to the principles taught in class 9, providing students with a tangible connection to their studies.
Engineering is another area where trigonometric problems manifest extensively. Engineers often apply trigonometry in fields such as civil, mechanical, and electrical engineering. For instance, when dealing with forces in a structure, trigonometric functions help in breaking down the forces acting at various angles, ensuring that the design can safely bear the load. This connection illustrates the significance of trigonometric principles learned in school.
Moreover, in astronomy, trigonometry plays a crucial role in gauging distances between celestial bodies and mapping the universe. Astronomers leverage concepts such as parallax, which relies on trigonometric principles, to measure the distance to nearby stars, enriching our understanding of space.
Additionally, in physics, trigonometric functions describe wave patterns and oscillations, integral concepts in topics like sound and light. Understanding these applications not only reinforces the theoretical aspects learned in class 9 but also strengthens the students’ motivation to explore trigonometry further.
In conclusion, the practical applications of trigonometry in architecture, engineering, astronomy, and physics exemplify its importance in various industries. By linking academic concepts to real-life scenarios, students can cultivate a deeper appreciation for trigonometric problems, thereby enhancing their learning experience in class 9 and beyond.